Huizenprijzen en aantal verkopen voorspellen met behulp van data science

Regressie

Zoals uitgelegd in de blog klantverloop verminderen door gebruik te maken van data science, is classificatie een krachtige methode om twee (of meer) entiteiten te scheiden op basis van hun kenmerken. In het voorbeeld van katten en honden gebruikten we variabelen zoals het slaapschema en het geluid dat ze produceren. Maar wat als we een continue numerieke waarde willen voorspellen, bijvoorbeeld de lengte van een persoon, in plaats van een binaire waarde? We kunnen de klassen waaruit het model kan kiezen aanzienlijk uitbreiden en ons nog steeds in het domein van de classificatie bevinden. Dit wordt ook wel de multiclass problems genoemd. Hierin kunnen we containers aanmaken, waarbij elke container een reeks waarden bevat. Een nadeel hiervan is dat je hiermee een oneindig aantal containers kunt krijgen. Zoals je je kunt voorstellen is dit niet efficiënt, gezien de tijd die dit in beslag neemt.

Een betere optie is regressie (regression). We gaan kijken naar een voorbeeld vanuit de statistiek. In dit geval zullen we ons op de linear regression focussen, omdat het de eenvoudigste en meest ongecompliceerde manier van regressie is. Logistic regression is technisch gezien ook een vorm van regressie, maar dan aangepast voor classificatie vraagstukken.

Voorbeeld 1: het voorspellen van de huizenprijzen

Okay, genoeg theoretische uitleg. We gaan nu kijken naar een voorbeeld. Wanneer we de huizenprijzen van een specifieke buurt willen voorspellen, kunnen we veel variabelen gebruiken. Meer variabelen betekent ook grotere vectoren voor de classificator. Houd er wel rekening mee dat te veel variabelen ruis kunnen veroorzaken in de classificator. Voor dit voorbeeld gebruiken we slechts één variabel: het vloeroppervlak in vierkante meters. Als we dit vertalen naar de statistiek, beschouwen we de variabel vloeroppervlakte in vierkante meters als onafhankelijk, terwijl de prijs van een huis de afhankelijke variabel is.

Met andere woorden, de prijs van een huis is direct gekoppeld aan het vloeroppervlak. We gaan ervan uit dat er een lineair verband bestaat tussen deze twee variabelen.

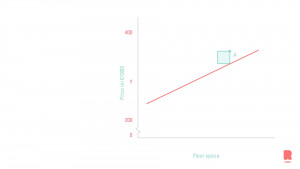
De horizontale as toont de variabelen van de dataset. In dit geval zou dat het vloeroppervlak zijn, de afhankelijke variabele. De prijs op de verticale as is hetgeen dat we willen voorspellen. Het figuur toont de best passende lijn voor ons model. Deze lijn moet als volgt worden gelezen; als we een huis in deze buurt hebben met een x hoeveelheid vloeroppervlak (horizontale as), dan geeft het snijpunt op de lijn ons de prijs van dit huis, weergegeven op de y-as (de verticale as).

Sum of Squares

Maar hoe weet het model welke lijn het beste past bij de gegevens? Misschien heb je inmiddels een klein groen vierkantje in het figuur opgemerkt. Dit vierkantje is de afstand van gegevenspunt A (wat we trainen) met de potentiële lijn voor het model. Deze afstand is gekwadrateerd, vandaar het kleine vierkantje, en telt alle andere datapunten in het figuur op. Dit proces wordt meerdere keren herhaald met verschillende potentiële modellijnen. Hoe kleiner de opgetelde waarde, hoe beter de lijn past. Let wel: dit is een zeer abstracte uitleg van de Sum of Squares methode.

Beperkingen van modellen met één onafhankelijke variabele

Bij grotere modellen staan er op de x-as meer variabelen (meer dimensies) om het model nog beter te laten presteren. Veel variabelen kunnen niet zo makkelijk worden getoond in figuren als hoe we net beschreven hebben. Nul variabelen (line), één variabel (2D-plot) en twee variabelen (3D-plot) kunnen in grafieken visueel getoond worden. Het tonen van meer dimensies is niet haalbaar op de gebruikelijke manieren. Door gebruik te maken van een model met één variabel heb je zelden de hoofdprijs te pakken, maar het dient wel als goed voorbeeld voor de uitleg.

Voorbeeld 2: het voorspellen van verkopen van een ijssalon

Laten we eens kijken naar een ander voorbeeld. We willen een numerieke waarde voorspellen, namelijk het aantal verkopen van een ijssalon. We hebben gegevens van een ijssalon in Rotterdam die haar verkoopcijfers van de afgelopen drie jaar heeft verzameld. De variabel aantal verkopen is de target variabel, hetgeen wat we willen voorspellen. We willen een algoritme trainen om te achterhalen en te begrijpen waarom de verkochte producten in de loop van de tijd verschilt.

Het verzamelen van externe gegevens

De gegevens van de ijssalon geven informatie over het aantal verkochte producten en wanneer de verkoop plaatsvond. Als we extra informatie willen, zullen we externe databronnen moeten raadplegen om de dataset uit te breiden. In dit geval kan het interessant zijn om gegevens over weersomstandigheden toe te voegen. Hoewel ik van ijs houd, eet ik het liever op een zonnige dag dan op een koude dag als het regent. Een andere interessante externe informatiebron zou de schoolvakantiekalender kunnen zijn, aangezien we verwachten dat meer gezinnen de ijssalon tijdens de vakantie zullen bezoeken.

Zodra we genoeg gegevens hebben verzameld om een betrouwbare voorspelling te doen, combineren we de interne en externe gegevensbronnen, zodat we een goede dataset hebben die gebruikt kan worden om ons algoritme te trainen. Zo zal bijvoorbeeld het lineaire regressiemodel  (linear regression model) een voorspelling genereren voor de komende 14 dagen. De weersverwachting voor de komende 14 dagen en de schoolvakantiekalender voor de komende 14 dagen zijn inputvariabelen (onafhankelijk) voor het model dat een voorspelling zal geven over de verwachte verkopen voor de ijssalon. Dit kan hem helpen met het plannen van personeel en het gerichter inkopen van voorraad.